神经网络的基本单元就是一个一个的感知机,感知机有两部分组成:线性部分和激活函数部分。一个感知机的能力是有限的,他只能将数据进行二分,而且这些数据还必须是线性可分的。
普遍逼近定理: 只要神经网络有一个隐藏层,它就可以任意逼近一个连续函数。这就让我想到了傅里叶级数,傅里叶级数其实就是把一个复杂的函数拆解成一个一个的圆周运动或者叫正弦波。神经网络也一样,他也是把一个复杂函数拆解成一个一个感知机。说到底就是一个线性函数+一个激活函数的形式。都是化复杂为简单。
傅里叶级数和神经网络很像,傅里叶级数用正弦函数去逼近任何一个波形,而神经网络是用感知机去逼近任何一个统计模型。为什么是统计模型呢?其实也好理解,那么多猫它们都是“猫神”模型的具象化,“猫神”模型再理念世界中它是可以没有误差的。但是只要一投射到现实世界里面,在现实世界它就有误差。所谓的分类,他其实就是在规定一个误差范围,在这个范围之内的它是猫,超过了就不是猫。猫具象化的误差肯定不是正态分布,如果是正态分布的话不会写不出来。那他的分布函数应该怎么写?参数是什么呢?这个时候就要用到神经网络,神经网络可以逼近任何一种统计模型。类似的,机器学习为什么又叫做统计学习。
思考: 神经网络会不会是新时代的“地心说”,为什么这么说呢?我们知道日心说是比地心说更好的,但这并不是说日心说比地心说更准确,而是它更简单。托勒密的地心说其实就是本轮+均轮,只要轮子够多它是可以逼近任何一条曲线的。因为它本质上就是一个傅里叶分解。当年哥白尼提出了日心说,大家普遍不接受,并不是不愿意相信太阳是中心,而是它预测的真的不准。后来,还是开普勒改变了基本范式,他把原来以圆为基础的范式,改成以椭圆为基础。结果呢,有简单有准确。
所以问神经网络会不会是新时代的“地心说”,其实就是想说未来会不会有一个像开普勒一样的人,他提出了一个新的范式。结果,原来我们要靠神经网络蛮力解决的一些问题,可以被它优雅简单地就给解决掉。
如何通俗易懂地解释遗传算法?有什么例子? - 知乎 (zhihu.com)
约翰·霍兰德:全宇宙第一个计算机博士,他做了一个基于元胞自动机和遗传算法做出来的,霍兰德也是遗传算法之父。
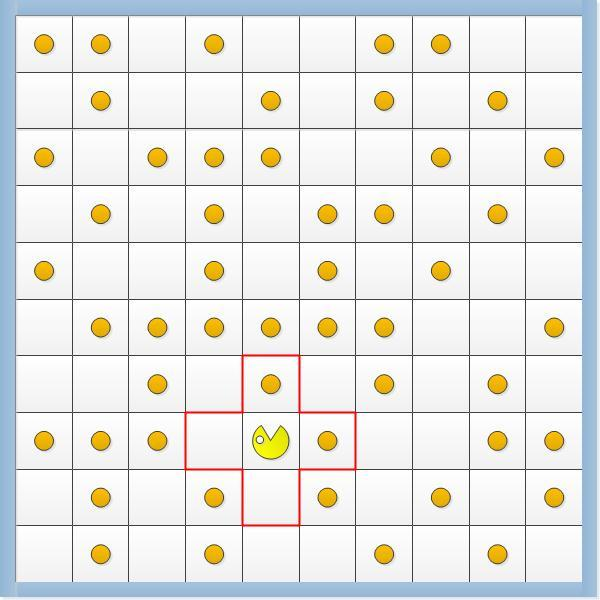
霍兰德想找出一个策略:就是让小机器人能吃最多的豆子,但是移动最少的动作。霍兰德找到了这样的最优策略,只不过这个最优策略是用遗传算法找到的。他一开始设计几条普普通通的策略,当然这个策略最后的得分肯定是惨不忍睹,霍兰德把其中最好的挑出来,然后让他们相互之间杂交、编译、遗传。最后经过很多代之后,最有策略就出现了。这个研究的结论很有意思:那个最优策略它无法被归约,就说这个策略没有办法用简单的、统一的方式给表示出来。其中机器人该如何做,只能按照特事特例的方式呈现出来,做一个集合做一个大表。
为什么这个策略没有办法被统一表示?而真是世界里的物理规律可以被统一表示呢?归根到底,这个策略是进化的产物,进化也就是演化。他是要优胜劣汰的,中间的每一个结果都要进行生存还是毁灭的价值判断。而物理规律呢?它是在发展但是不是在演化。他只是把底层规律进行了组合,并没有谁去判断这个规律的组合到底是好还是坏,没有这样的价值判断。
前面一直在强调激活函数的重要性,说他提供了价值观。如果没有激活函数,只有线性函数会怎样?线性函数不论嵌套多少层,都是一个简单的线性函数,都能被统一表示。但是一旦有了激活函数,事情就不一样了。有了激活函数之后,就有了价值判断。它描述的事情,就没有办法再被简单的表示了。
所以神经网络会是新时代的“地心说”吗?我觉得不会,面对我们人类进化而来的智能,也许神经网络这种无限逼近真相的这个范式已经是最好的范式了。当然,这部分只是我开脑洞。