$FGD$ 小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。
为了能够对旅程有一个安排,他想知道山峰和山谷的数量。
给定一个地图,为 $FGD$ 想要旅行的区域,地图被分为 $n×n$ 的网格,每个格子 $(i,j)$ 的高度 $w(i,j)$ 是给定的。
若两个格子有公共顶点,那么它们就是相邻的格子,如与 $(i,j)$ 相邻的格子有 $(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)$。
我们定义一个格子的集合 $S$ 为山峰(山谷)当且仅当:
$S$ 的所有格子都有相同的高度。
$S$ 的所有格子都连通。
对于 $s$ 属于 $S$,与 $s$ 相邻的 $s′$ 不属于 $S$,都有 $w_s > ws′$(山峰),或者 $w_s < w_s′$(山谷)。
如果周围不存在相邻区域,则同时将其视为山峰和山谷。
你的任务是,对于给定的地图,求出山峰和山谷的数量,如果所有格子都有相同的高度,那么整个地图即是山峰,又是山谷。
输入格式
第一行包含一个正整数 $n$,表示地图的大小。
接下来一个 $n×n$ 的矩阵,表示地图上每个格子的高度 $w$。
输出格式
共一行,包含两个整数,表示山峰和山谷的数量。
数据范围
$1 ≤ n ≤ 1000$,
$0 ≤ w ≤ 10^9$
输入样例1:
5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8输出样例1:
2 1输入样例2:
5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7输出样例2:
3 3样例解释
样例1:

样例2:
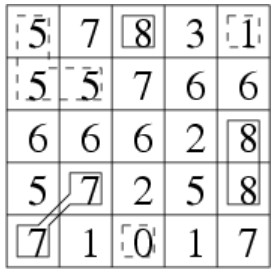
题解:
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N =1010;
int g[N][N];
bool st[N][N];
typedef pair<int,int> pii;
int n;
void bfs(int sx, int sy, bool& has_higher, bool& has_lower) {
queue<pii> que;
que.push({sx, sy});
st[sx][sy] = true;
while(!que.empty()) {
auto cur = que.front(); que.pop();
for(int i = cur.first-1; i <= cur.first+1; i++) {
for(int j = cur.second-1; j <= cur.second+1; j++) {
if(i == cur.first && j == cur.second) continue;
if(i < 0 || i >= n || j < 0 || j >= n) continue;
if(g[i][j] != g[cur.first][cur.second]) {
if(g[i][j] > g[cur.first][cur.second]) has_higher = true;
else has_lower = true;
}else if(!st[i][j]){
que.push({i, j});
st[i][j] = true;
}
}
}
}
}
int main() {
cin >> n;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
cin >> g[i][j];
}
}
int h = 0, l = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(!st[i][j]) {
bool has_higher = false, has_lower = false;
bfs(i, j, has_higher, has_lower);
if(!has_higher) h++;
if(!has_lower) l++;
}
}
}
cout << h << " " << l << endl;
return 0;
}