编辑距离(列文斯登距离)
输入: AUDI,LADA
输出:LA-DA, AUDI
3 个操作:删除 L, 插入 U, 把 A 替换成 I.
定义
给定两个序列 x 和 y,需要多少次增、删、改的操作,才能把 x 变成 y?在 unix 命令 diff 中,这段距离显示为两个给定文件中的对应行之间相互变换所需的最少操作次数。
时间复杂度为 O(nm) 的算法
对 n = |x|, m = |y| 使用动态规划法,算法时间复杂度为 O(nm)。我们要计算一个数组 A[i,j],它是长度为 i 的前缀 x 和长度为 j 的前缀 y 之间的距离。我们从初始化开始,定义 A[0,j] = j 和 A[i,0] = i。一般情况下,当 i 和 j 都 $\geq$ 1,前缀的最后几个字母有三种可能情况:$x_{i}$ 被删除;$y_{i}$ 被插入到尾部; $x_{i}$ 和 $y_{i}$ 替换(如果它们不相同)。这三种情况让我们可以用递归方式定义以下三个公式:
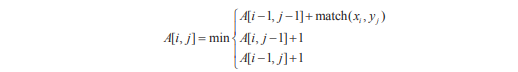
其中 match 是一个返回布尔值的函数,当两个参数不相等时,函数会返回 1.这个方法定义了替换一个字母的成本。成本是可以调整的,比如说,成本可能取决于键盘上的距离。
操作序列
除了计算编辑距离,还要计算把 x 变换成 y 所需的操作次数。我们可以使用在图中查找最短路径的方式。通过遍历所有来路节点的距离,我们就能找到通向顶端的一条最短路径。这样一来,我们就能从节点(n,m)一直上升到(0,0),并在上升的沿途路径中,计算出最优方案的所有操作步骤。最后,只要把这个序列逆序排列即可得到答案。
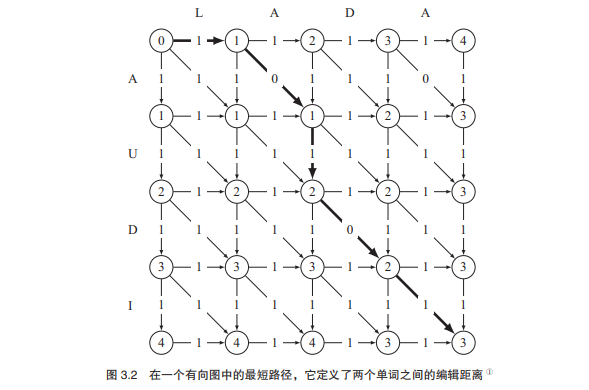
注意: 竖排字符串是 AUDI,横排字符串是 LADA。从左上到右下的操作是:删除 L,距离 1;A 不
变,距离 0;插入 U,距离 1;D 不变,距离 0;A 替换成 I,距离 1。最短路径的 5 个步骤是 1-0-1-
0-1。
实现细节
在动态规划中,图的下标从 0 开始,而两个待变换字符串的下标从 1 开始。在实现的时候要注意这一点。
def levenshtein(x, y):
n = len(x)
m = len(y)
# 初始化第 0 行和第 0 列
A = [[i+j for j in range(m+1)] for i in range(n+1)]
for i in range(n):
for j in range(m):
A[i+1][j+1] = min(A[i][j+1] + 1, # 插入
A[i+1][j] + 1, # 删除
A[i][j] + int(x[i] != y[j])) # 替换
return A[n][m]深入思考
在实际应用中,人们已经提出了性能更好的算法。比如,如果已知两个字符串编辑距离的长度上限 s,我们可以吧上述动态规划,矩阵 A 的对角线长度限制为最大编辑距离 s,从而得到一个时间复杂度为 O(s min{n,m}) 的算法(见参考文献)。