混淆矩阵
| pred positive | pred negative | |
|---|---|---|
| actual positive | TP | FN |
| actual negative | FP | TN |
True和False是真实的标签,positive和negative是预测的值
- 真阳性(TP):诊断为有,实际上也有高血压。
- 伪阳性(FP):诊断为有,实际却没有高血压。
- 真阴性(TN):诊断为没有,实际上也没有高血压。
- 伪阴性(FN):诊断为没有,实际却有高血压。
准确率 Accruacy
准确率非常好理解,预测对的样本占总样本的比例,正的预测为正的,负的预测为负的
到这里其实很符合逻辑,但是又一个小问题,不是评价指标的问题,是模型的问题,那就是样本不均衡,例如有一个数据集,正样本只有1个,负样本有99个,直接把所有的样本预测为负就可以了,acc=99/100=99%,这很明显是不合理的。其实我们想要的是,预测的正样本尽可能都是正样本,预测的负样本尽可能都是负样本。
精确率(P)和召回率(R)
精确率:预测的正样本中有多少是预测对的
召回率:实际的正样本有多少是被预测对了
从名字就很好区分,
- 召回率召回率就是找回率,实际的正样本中找回了多少个正样本,猫狗分类里面,有100只小猫咪,你找回了几只,这就是找回率(召回率)
- 精确率就是说,你判断除100只小猫咪,里面到底有多少真的是猫咪,你说的有多准
我们知道,在做分类的时候,是有一个概率阈值的,例如0.5,预测的概率大于0.5,判断成正类,小于0.5就判断成负类,我们修改阈值的时候,预测的结果就会发生变化,
PR之间的矛盾
精确率和召回率是一对矛盾的指标,一般来说,精确率高的时候召回率会低,反之亦然。假如你训练了一个猫狗分类器,你想要预测的结果尽可能精确,预测的猫一定是猫,你该怎么办呢,最简单的办法就是提高分类时的阈值,例如原来区分猫狗的阈值是0.5,现在你把阈值提升到0.9,那基本上预测的猫就都是猫了。如果你想要提升召回率怎么办呢?就是说把样本中的猫尽可能的都找回来,那简单,全都预测成猫就行了。
在一些应用中,对查准率和查全率的重视程度有所不同。例如在商品推荐系统中,为了尽可能少打扰用户,更希望推荐内容确实是用户感兴趣的,此时查准率更重要;而在逃犯信息检索系统中,更希望尽可能少漏掉逃犯,此时查全率更重要。
PR曲线
在很多情形下,我们可根据学习器的预测结果对样例进行排序,排在前面的是学习器认为“最可能”是正例的样本,排在最后的是学习器认为“最不可能”是正例的样本。按此顺序设置不同的阈值,逐个把样本作为正例进行预测,则每次可以计算出当前的查准率、查全率。以查准率为纵轴、查全率为横轴作图,就得到了查准率-查全率曲线,简称“P-R曲线”,显示该曲线的图称为“P-R图”。
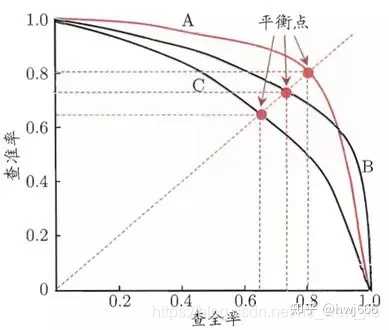
如果我们训练了多个模型,想要比较哪个模型效果更好,一开始我们可以直接看准确率,现在我们可以评估精确率和召回率,并且通过调整不同的阈值可以实现pr曲线来进行对比,如果一条曲线A完全包住了另一条曲线B,那么我们认为A模型性能好于B模型。如果发生了交叉,则难以比较,我们可以对比PR曲线下的面积。它在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。
ROC曲线
PR曲线已经可以很好的解决模型评估的问题了,但是还是有问题,当样本不平衡的时候,PR曲线依然会失真。我们可以使用ROC曲线进行评估
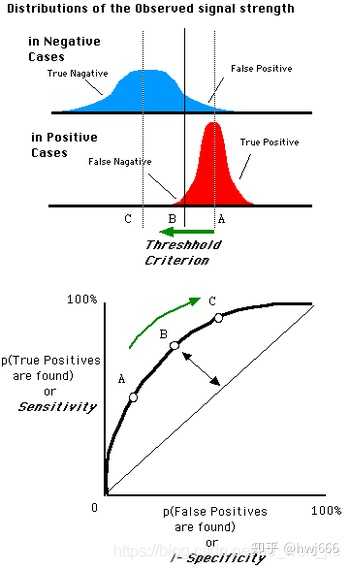
ROC曲线起源于第二次世界大战时期雷达兵对雷达的信号判断。当时每一个雷达兵的任务就是去解析雷达的信号,但是当时的雷达技术还没有那么先进,存在很多噪声(比如一只大鸟飞过),所以每当有信号出现在雷达屏幕上,雷达兵就需要对其进行破译。有的雷达兵比较谨慎,凡是有信号过来,他都会倾向于解析成是敌军轰炸机,有的雷达兵又比较神经大条,会倾向于解析成是飞鸟。这个时候,雷达兵的上司就很头大了,他急需一套评估指标来帮助他汇总每一个雷达兵的预测信息,以及来评估这台雷达的可靠性。
对于ROC曲线,它是“真正例率”(True Positive Rate, 简称TPR),横轴是“假正例率”(False Positive Rate,简称FPR)的关系曲线,计算式如下:
真正例率是在所有正例中,你将多少预测为了正例,这是你希望最大化的,也可以看作收益;假正例率是在所有负例中,你又将多少预测为了正例,这是你希望最小化的,也可以看作代价。
从公式(2)和表中可以看出,TPR考虑的是第一行,实际都是正例,FPR考虑的是第二行,实际都是负例。因此,在正负样本数量不均衡的时候,比如负样本的数量增加到原来的10倍,那TPR不受影响,FPR的各项也是成比例的增加,并不会有太大的变化。因此,在样本不均衡的情况下,同样ROC曲线仍然能较好地评价分类器的性能,这是ROC的一个优良特性,也是为什么一般ROC曲线使用更多的原因。
而看公式(1)和表,精确率P考虑的是第一列,实际中包括正例和负例,因此,正负样本数量的变化会引起该值的变化,进而影响PR曲线对分类器的评价。
曲线下面积(AUC)
简单来说其实就是随机抽出一对样本(一个正样本,一个负样本),然后用训练得到的分类器来对这两个样本进行预测,预测得到正样本的概率大于负样本概率的概率。
在有M个正样本,N个负样本的数据集里。一共有MN对样本(一对样本即,一个正样本与一个负样本)。统计这MN对样本里,正样本的预测概率大于负样本的预测概率的个数。
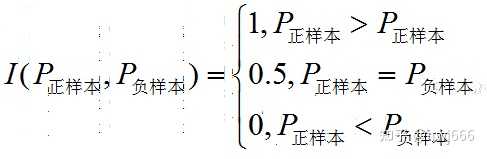
还有一种计算方法是
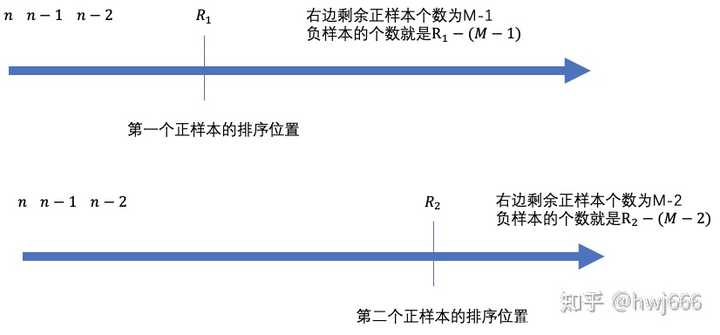
我画了一个图来解释这个公式是什么意思,首先我们将所有样本按照预测的概率值,从大到小的数据进行排序,最大的那个样本编号为n,依次递减,假设有M个正样本。
- 对于第一个正样本,我们假设排序后的位置是 $R_1$ ,那么此时,第一个正样本右边还有$M-1$ 个正样本,那么右边还有 $R_1-1-(M-1)$ 个负样本,也就是说选择第一个正样本时,会有 $R_1-1-(M-1)$ 个负样本小于正样本.
- 同理假设第二个负样本排序后的位置为 $R_2$ ,第二个正样本右边还有 $M-2$ 个正样本,那么右边还有 $R_2-1-(M-2)$ 个负样本
- 对于第i个正样本排序后位置是 $R_i$ ,右边还有 $M-i$ 个正样本,那么右边还有 $R_i-(M-i)$ 个负样本
递归计算后可知
做一个简单的变换后可知