最长公共子序列
输入:GAC,AGCAT
输出:A G C A T
| |
G A C
定义
设一个符号集合 $\sum$ 。对于两个序列 $s, x \in \sum \star$,果存在下标 $i_{1}$ <…< $i_{|s|}$ 使得对于所有 $x_{ik} = s_{k}$,且其中 k = 1,…, |s|,那么我们定义 s 是 x 的子序列。假设有两个序列 $s, x \in \sum \star$ , 需要找到长度最大的子序列 $s \in \sum \star$, 而且它同时是 x 和 y 的子序列。
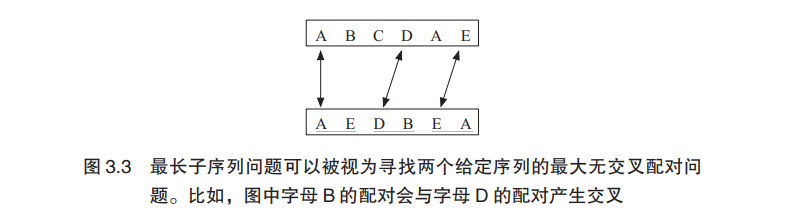
问题的另外一个表述方式为“配对”(见 9.1 节)。我们在两个序列 x 和 y 中寻找配对的最大可能性,使得这两个序列中的字母配对连线不交叉(图 3.3)。
应用
在一个文件同步系统中,为了最小化网络传输流量,我们希望仅发送被修改过的部分,而不是把文件完整地发送到服务器。为了满足这个需求,必须找到旧文件和新文件的最大公共子序列。
这类问题同样出现在生物信息学中,用于对齐两条 DNA 序列。
时间复杂度为 O(nm) 的算法
当 n = |x| 和 m = |y| 时,对于所有 $0 ≤ i ≤ n$ 和 $0 ≤ j ≤ m$ ,我们计算前缀 $x_{1} … x_{i}$ 和 $y_{1} … y_{j}$ 的最长
公共子序列。这就得到一个复杂度为 $n·m$ 的子问题。基于 (i-1, j)、(i, j-1) 和 (i-1, j-1) 在常数时间内得到的解,就能得到 (i, j) 的最优解。因此,我们可以在时间 O(nm) 内解决问题 (n, m)。算法基于以下测试结果。
关键测试
设序列 $x_{1}, … , x_{i}$ 和 $y_{1}, … , y_{j}$ 的最长公共子序列为$ A[i, j]$。在 $i = 0$ 或 $j = 0$ 时,$A[i, j]$ 为空。当 $x_{i} ≠ y_{j}$ 时,$x_{i}$ 和 $x_{j}$ 中的一个肯定不在最优解中,而且 $A[i, j]$ 是 $A[i-1, j]$ 和 $A[i, j-1]$ 中最长的序列 $A$。当 $x_{i} = y_{j}$ 时,存在一个最优解使得字符相关,而且 $A[i, j]$ 等于 $A[i-1, j-1] · x_{i}$。这里的符号 “·” 表示字符串拼接。使用 $maximum$ 函数可以让最长序列延伸 $B$。
def longest_common_subsequence(x, y):
n = len(x)
m = len(y)
# 计算最优长度
A = [[0 for j in range(m + 1)] for i in range(n + 1)]
for i in range(n):
for j in range(m):
if x[i] == y[j]:
A[i + 1][j + 1] = A[i][j] + 1
else:
A[i + 1][j + 1] = max(A[i][j + 1], A[i + 1][j]) # 输出结果
sol = []
i, j = n, m
while A[i][j] > 0:
if A[i][j] == A[i - 1][j]:
i -= 1
elif A[i][j] == A[i][j - 1]:
j -= 1
else:
i -= 1
j -= 1
sol.append(x[i])
return ''.join(sol[::-1]) # 列表反转注:
- 因为是两个序列比较,所以是比长短而不是大小。
- 当 $x_{i} = y_{j}$ 时,如果两个序列最后一个元素不一样,那么这两个元素中肯定有一个不在最终结果中,而且最优解一定等于各少一个元素的子序列中较长的那一个:$A[i-1, j]$ 是从 $A[i, j]$ 去掉 $x_{i}$,$A[i, j-1]$ 是从 $A[i, j]$ 去掉 $y_{j}$。这里的思路也是把大问题拆分成小问题:想找到 $A[i, j]$,可以先尝试找 $A[i-1, j]$ 和 $A[i, j-1]$, 一步步缩短目标序列,从而简化问题。——译者注
变种1:给定多个序列
假设我们不是从两个序列而是从 k 个序列中寻找最长公共子序列,序列长度分别为 $n_{1}, … , n_{k}$,那么可以使用以下方法。我们需要计算一个 k 维矩阵 A,计算所有给定序列的前缀组合产生的最长公共子序列。这个算法的时间复杂度是 $O(2^{k}\prod_{i-1}^{k} n_{i})$ 。
变种2:给定两个排好序的序列
当两个序列都已经排好序时,问题可以在时间 O(n+m) 内解决。因为在这种情况下,我们可以使用合并两个已排序队列的方法(见 4.1 节)。
实践
使用 BLAST 算法(Basic Local Alignment Search Tool),但它不能保证总是得出最优解。