N 皇后

标签 ：Algorithm

$n$ 皇后问题研究的是如何将 $n$ 个皇后放置在 $n×n$ 的棋盘上，并且使皇后彼此之间不能相互攻击。

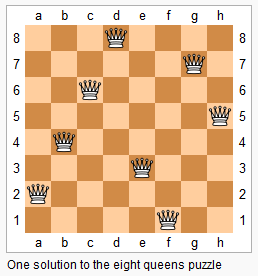
上图为 8 皇后问题的一种解法。

给定一个整数 $n$，返回所有不同的 $n$ 皇后问题的解决方案。

每一种解法包含一个明确的 $n$ 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],

["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

Answers 1:

class Solution:
    def solveNQueens(self, n): # 使用回溯法
        ans = [] # 包含所有情况的 solutions
        
        def dfs(nums, row): 
            if row == n:
                # path 记录的是前 row 行的放置位置，
                # 一旦 row == n，就代表整个棋盘的放置位置已经确定
                ans.append(nums[:])
                return
            for col in range(n):  # 对于某行的各个列
                nums[row] = col  # nums[row] 记录第 row 行 queen 所在的列数
                if valid(nums, row):  # 检查把 row 行 i 列放上 queen 之后，这个 row 是否合法
                    dfs(nums, row+1)
                    
        def valid(nums, row):
            for i in range(row):  # i 指的是 row 前面的行
                if abs(nums[i]-nums[row]) == abs(row - i) or nums[i] == nums[row]:
                    # i 行和 row 行的 queen 在对角线上  or i 行和 row 行的 queen 在同一列上
                    return False
            return True
        
        dfs([None for _ in range(n)], 0)
        
        # Draw the graph
        result = [[] for _ in range(len(ans))]
        for i in range(len(ans)):
            for col in ans[i]:
                tmp = '.' * n
                result[i].append(tmp[:col] + 'Q' + tmp[col+1:])
        return result

Answers 2:

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res = []
        s = "." * n
        def backtrack(i, tmp,col,z_diagonal,f_diagonal):
            if i == n:
                res.append(tmp)
                return 
            for j in range(n):
                if j not in col and i + j not in  z_diagonal and i - j not in f_diagonal:
                    backtrack(i+1,tmp + [s[:j] + "Q" + s[j+1:]], col | {j}, z_diagonal |{i + j} , f_diagonal |{i - j}  ) 
            
        backtrack(0,[],set(),set(),set())    
        return res