初等数论与组合数学初步
引言
数论部分是 ACM 竞赛中最难的部分之一,本文仅作入门学习参考之用,文中省略了某些复杂定理的证明,详细证明过程请参考其他资料,文中的扩展欧几里得算法和中国剩余定理并不常用,供学有余力的同学学习
1. 同余
1.1 带余除法
1.1.1 定义 带余除法 设 a, b 是整数,且 b>0 ,则存在非负整数 q, r ,使得
$$a = bq + r$$
且 $0≤ r < b$, 称 q 为商, r 为余数
显然带余除法中的商和余数都是唯一的,在下文中将商记为 $a/b$ ,将余数记为 $a%b$,“/” 与 “%”的运算优先级与乘除法相同,当然,在 C 语言中二者分别对应 $a/b$ 与 $a%b$
注意到被除数 a 是可以为负数的,但如无特殊说明,下文不考虑负数
1.2 同余方程
1.2.1 定义 同余方程 设 a,b 是整数,若它们除以正整数 m 的余数相同,则称 a,b 对于模 m 同余,记为
$$a ≡ b (mod m)$$
1.3 “+”、“-”、“×”的取余运算
1.3.1 性质 加法的取余运算
$$(a+b)%c=(a%c+b%c)%c$$
证 $$(a+b)%c=((a/c)c+a%c+(b/c)c+b%c)%c=(a%c+b%c)%c$$
用类似的方法可以证得
1.3.2 性质 减法的取余运算
$$(a−b)%c=(a%c−b%c+c)%c$$
1.3.3 性质 乘法的取余运算
$$(ab)%c=(a%c)(b%c)%c$$
注意到 1.3.2 性质中等式右边加了 c ,是因为 a 可能是负数,为了便于写代码,将其处理成非负数
1.4 逆元
虽然取余运算对于“+”、“-”、“×”不难,但通常情况下
$$\frac{a}{b}%c ≠ \frac{a%c}{b%c}%c$$
如何计算 $\frac{a}{b}%c$ ?我们通常要找一个逆元 $b^{−1}$ ,使得 $bb^{−1} ≡ 1 ( mod c)$ ,那么就有
$$\frac{a}{b}%c = ab^{−1}%c$$
如果 c 是素数,根据下面的定理
1.4.1 费马小定理 设 b 是一个整数,c 是一个素数,那么
$$b^{c−1} ≡ 1 (mod c)$$
定理的证明需要引入简化剩余系的概念,略显复杂,此处省略
将上式改写一下,得到
$$bb^{c−2} ≡ 1 (mod c)$$
因此取 $b^{−1} = b^{c−2}$ 即可,一般需要用快速幂计算,但要注意,与除数不能为 0 类似,要保证 $b % c ≠ 0$
至于 c 不是素数的情况,有时逆元甚至不存在,如果存在,可用扩展欧几里得算法计算,将在下面 3 中介绍,如果不存在,可以考虑不求逆元,直接使用高精度计算 $\frac{a}{b}$
2. 最大公因数与最小公倍数
2.1 最大公因数
顾名思义,最大公因数就是公因数中最大的那个,我们记 a, b 的最大公因数为 $gcd(a,b)$,有如下性质
- 2.1.1 性质 gcd(a,b)=gcd(b,a)
- 2.1.2 性质 gcd(a,b)=gcd(a−b,b)(a≥b)
- 2.1.3 性质 gcd(a,b)=gcd(a%b,b)
- 2.1.4 性质 gcd(a,b,c)=gcd(gcd(a,b),c)
2.1.1 性质是显然的,2.1.2 性质是辗转相减法的原理,2.1.3 性质可以视为2.1.2 性质的“一步到位”版本,2.1.4 性质指出多个数的最大公因数可以递推地进行求解
2.2 辗转相除法
根据2.1.3 性质,得到辗转相除法的参考代码模板
typedef long long ll;
ll gcd(ll a, ll b){
return b?gcd(b,a%b):a;
}注意当 $b ≠ 0$ 时,返回值为 $gcd(b,a%b)$ 而不是 $gcd(a%b,b)$ ,否则会不断递归导致栈溢出
2.3 最小公倍数
顾名思义,最小公倍数就是公倍数中最小的那个,我们记 a, b 的最小公倍数为 $lcm(a,b)$,有如下性质
2.3.1 性质
$$lcm(a,b) = \frac{ab}{gcd(a,b)}$$
下面是最小公倍数的参考代码模板
ll lcm(ll a, ll b){
return a/gcd(a,b)*b;
}注意是先除后乘,避免在中间过程中数据超出64位整数的范围
3. 扩展欧几里得算法
3.1 扩展欧几里得算法
考虑方程
$$ax + by = c$$
其中 $a, b, c$ 是已知的正整数,如何求出方程的解呢?
3.1.1 定理 上述方程有解的充要条件是 $gcd(a,b)|c$ (c 是 gcd(a,b) 的倍数)
证明过程暂时省略
我们先将问题简化,求方程
$$ax + by = d$$
的解,其中 a,b 是正整数, $d = gcd(a, b)$
前文中所述的辗转相除法又名欧几里得算法,扩展欧几里得算法就是在此基础上实现的,下面举例来描述算法的过程
例 求方程 $36x + 28y = 4$ 的解
- 36 = 28 × 1 + 8
- 28 = 8 × 3 + 4
- 8 = 4 × 2
将前两步改写一下:
- 8 = 36 − 28 × 1
- 4 = 28 − 8 × 3
再代入一下,得
4 = 28 − (36 − 28 × 1) × 3 = 28 × 4 + 36 × (−3)
因此 $x=−3,y=4$ 是方程的一组解,方程的任一解可以表示成
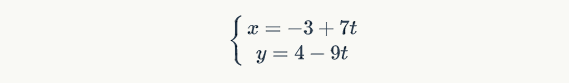
更一般地,方程 $ax+by=d,d=gcd(a,b)$ 的所有解为
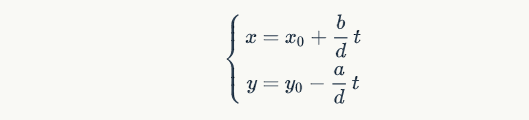
其中 $x_{0}, y_{0}$ 是一组特解
回到最开始的问题,方程 $ax+by=c,gcd(a,b)|c$ 的所有解为
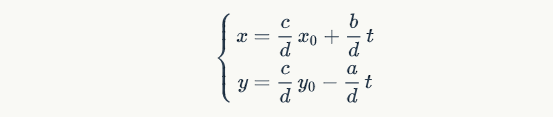
其中 $x_{0}, y_{0}$ 是方程 $ax + by = d, d = gcd(a, b)$ 的一组特解
下面是参考代码模板:
ll ext_gcd(ll a,ll b,ll& x,ll& y){
ll d = a;
if (!b){
x = 1;y = 0;
}else{
d = ext_gcd(b,a%b,y,x);
y -= a/b*x;
}
return d;
}3.2 扩展欧几里得算法与逆元
回到1.4中挖的坑,要找到 $b^{−1}$ 使得 $bb^{−1} ≡ 1( mod c)$ ,实质上是求解方程 $bx + cy = 1$ 中的 $x$ ,当然只有 $gcd(b,c) = 1$ 时才有解,否则逆元不存在
4. 同余方程组与中国剩余定理
有神就有光,有方程就有方程组

其中 $a_{1}, a_{2}, …, a_{n}$ 是整数, $m_{1}, m_{2}, …, m_{n}$ 是正整数
4.1.1 中国剩余定理(孙子定理) 设上述方程组中 $m_{1}, m_{2}, …, m_{n}$ 两两互质,则方程组的通解为
$$x = k \prod_{i=1}^{n}m_{i} + \sum_{i=1}^{n}a_{i}M_{i}M_{i}^{-1}$$
其中 $M_{i} = \prod_{j≠i} m_{j}$
定理的证明过程暂时省略
下面是参考代码模板,需要调用前面的扩展欧几里得算法模板
ll Sunzi(ll *m,ll *a,int len){
ll lcm = 1;
ll ans = 0;
for (int i=0;i<len;i++){
ll k0,ki;
ll d = ext_gcd(lcm,m[i],k0,ki);
if ((a[i]-ans)%d!=0) return -1;
else {
ll t = m[i]/d;
k0 = ( k0*(a[i]-ans)/d%t + t)%t;
ans = k0*lcm + ans;
lcm = lcm/d*m[i];
}
}
return ans;
}5. 素数
素数是只有 1 和它本身两个因数的数,1 不是素数
5.1 素数的判断
bool isPrime(ll n){
if(n==1)return false;
for(ll i=2;i*i<=n;i++)
if(n%i==0)return false;
return true;
}这是最简单的素数的判断的参考代码模板,复杂度为 $O(\sqrt{n})$
原理其实很简单,对于一个大于 1 的整数,如果 x 是它的一个大于 $\sqrt{n}$ 的因子,那么 $\frac{n}{x}$ 是它的小于 $\sqrt{n}$ 的因子
在大多数情况下,这种判断方式的复杂度已经足够小了,如果要吹毛求疵追求更低的复杂度,可以使用下面的方法
bool isPrime(ll n){
if(n==2||n==3||n==5)return 1;
if(n%2==0||n%3==0||n%5==0||n==1)return 0;
ll c=7,a[8]={4,2,4,2,4,6,2,6};
while(c*c<=n)for(auto i:a){if(n%c==0)return 0;c+=i;}
return 1;
}这种方法至少能保证int范围内的数是正确的,当 n 过大时可能会出错,笔者暂时还不知道最小的会出错的数是多少
5.2 素数筛
如果要求出不超过 n 的所有素数,素数筛是最好的选择,下面是一种朴素的筛法
void getPrime(bool p[],int n){
for(int i=1;i<=n;i++)p[i]=true;
p[1]=false;
for(int i=2;i<=n;i++){
if(p[i]){
for(int j=i+i;j<=n;j+=i)p[j]=false;
}
}
}这种方法的原理是从小到大将素数的倍数筛掉,复杂度为 $O(nlogn)$ ,注意到每个合数如果有多个素因子,那么就会被重复筛掉,造成复杂度的浪费,因此,用下面的方法可以保证每个合数只被它最小的素因子筛掉一遍,以 $O(n)$ 的复杂度解决上述问题
ll getPrime(ll n,bool vis[],ll prime[]){
ll tot=0;
for(ll i=1;i<=n;i++)vis[i]=0;
for(ll i=2;i<=n;i++){
if(!vis[i])prime[tot++]=i;
for(ll j=0;j<tot;j++){
if(prime[j]*i>n)break;
vis[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
return tot;
}上述代码可能略显难懂,笔者也不知如何讲清原理,请读者仔细体会
6. 组合数学初步
6.1 组合数
4.1.1 定义 组合数 在 $n(n≥0)$ 个不同元素中选取 $m(0≤m≤n)$ 个元素,不同的取法记为
$$C_{n}^{m} = \frac{n!}{m!(n-m)!}$$
6.2 杨辉三角
组合数与杨辉三角中的数字是一一对应的

杨辉三角的自然数形式

杨辉三角的组合数形式
按照上面的写法,杨辉三角的第 $n$ 行第 $m$ 列即为 $C_{n+m−2}^{m−1}$
注意到上图中每个数等于其左边的数与上边的数(如果有的话)之和,这就是杨辉恒等式
$$C_{n}^{m} = C_{n−1}^{m-1} + C_{n−1}^{m}$$
6.3 组合数的取余计算
在 ACM 竞赛中,我们常常需要计算 $C_{n}^{m}%p$ ,可以参考下面两种方法
如果 $n, m$ 不大,可以开 $O(n^{2})$ 的空间,可以利用杨辉恒等式来预处理组合数表
const ll mo=1e9+7;
ll C[1005][1005];
void getC(int n){
for(int i=0;i<=n;i++){
for(int j=0;j<=i;j++){
if(j==0 || j==i)
C[i][j]=1;
else
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mo;
}
}
}如果 $n, m$ 比较大,可以开 $O(n)$ 的空间,可以利用前文所述的逆元来求解,当然,要保证 $p$ 是素数
const ll mo=1e9+7;
ll C(ll n,ll m){
static ll M=0,inv[N],mul[N],invMul[N];
while(M<=n){
if(M){
inv[M]=M==1?1:(mo-mo/M)*inv[mo%M]%mo;
mul[M]=mul[M-1]*M%mo;
invMul[M]=invMul[M-1]*inv[M]%mo;
}
else mul[M]=1,invMul[M]=1;
M++;
}
return mul[n]*invMul[m]%mo*invMul[n-m]%mo;
}上面的代码中用 $O(n)$ 的复杂度处理了 $[1,n]$ 的逆元(原理在此不深究,当然读者可以使用上文中提到的用快速幂求逆元的方法,在大多数情况下足够了),处理 $Q$ 次 $n, m ≤ N$ 的询问的总复杂度为 $O(N+Q)$
附录
题目列表
- codeforces 1108B Divisors of Two Integers 想法题
- codeforces 299A Ksusha and Array 最大公因数
- codeforces 1033B Square Difference 素数
- codeforces 822A I’m bored with life 最大公因数
- codeforces 131C The World is a Theatre 组合数
- codeforces 898B Proper Nutrition 扩展欧几里得
这些题目应该都不难
……
吧