一. 蒙特卡罗方法

蒙特卡罗是什么？

赌城！蒙特卡洛是摩纳哥公国的一座城市，位于欧洲地中海之滨、法国的东南方，属于一个版图很小的国家摩纳哥公国，世人称之为“赌博之国”、“袖珍之国”、“邮票小国”。蒙特卡洛的赌业，海洋博物馆的奇观，格蕾丝王妃的下嫁，都为这个小国增添了许多传奇色彩，作为世界上人口最密集的一个国度，摩纳哥在仅有1.95平方千米的国土上聚集了3.3万的人口，可谓地窄人稠。但相对于法国，摩纳哥的地域实在是微乎其微，这个国中之国就像一小滴不慎滴在法国版图内的墨汁，小得不大会引起人去注意它的存在。蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的曼哈顿计划时首先提出，为保密选择用赌城摩纳哥的蒙特卡洛作为代号，因而得名。

看到这里，你可能似乎已经意识到，这个方法一定和赌博，概率分布，近似数值计算有着千丝万缕的联系。事实的确如此，首先我想引用一段李航老师在《统计学习方法》中关于MCMC的介绍：

蒙特卡罗法(Monte Carlo method)，也称为统计模拟方法(statistical simulationmethod)，是通过从概率模型的随机抽样进行近似数值计算的方法。

马尔可夫链蒙特卡罗法(Markov Chain Monte Carlo，MCMC)，则是以马尔可夫链(Markovchain)为概率模型的蒙特卡罗法。马尔可夫链蒙特卡罗法构建一个马尔可夫链，使其平稳分布就是要进行抽样的分布，首先基于该马尔可夫链进行随机游走，产生样本的序列，之后使用该平稳分布的样本进行近似的数值计算。

Metropolis-Hastings 算法是最基本的马尔可夫链蒙特卡罗法，Metropolis 等人在 1953 年提出原始的算法，Hastings 在1970 年对之加以推广，形成了现在的形式。吉布斯抽样(Gibbs sampling)是更简单、使用更广泛的马尔可夫链蒙特卡罗法，1984 年由S. Geman 和D. Geman 提出。

马尔可夫链蒙特卡罗法被应用于概率分布的估计、定积分的近似计算、最优化问题的近似求解等问题，特别是被应用于统计学习中概率模型的学习与推理，是重要的统计学习计算方法。

相信读完这一段大多数人都依然懵逼，我们一个概念一个概念地介绍，对于任何一种方法，我们会先阐明它在生活中的用途，让读者有个总体的认识，再去推导它的数学原理，让它彻底地为你所用。

从蒙特卡洛方法说起

生活中的例子：

• 1.蒙特卡罗估计圆周率 $\pi$ 的值

绘制一个单位长度的正方形，并绘制四分之一圆。在正方形上随机采样尽可能多的点，放上 3000 次，就可以得到如下这张图：

蒙特卡罗估计圆周率

洒完这些点以后，圆周率的估计值就很明显了：

$$\pi = \frac{4N}{3000}$$

其中 $N$ 是一个数据点放在圆内部的次数。

• 2.蒙特卡罗估计任意积分的值

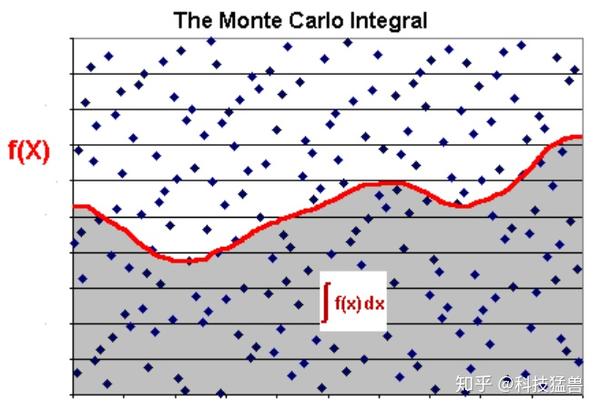
蒙特卡罗估计任意积分的值

在该矩形内部，产生大量随机点，可以计算出有多少点落在阴影部分的区域，判断条件为 $y_i < f(x_i)$ ，这个比重就是所要求的积分值，即：

$$\frac{N_{阴影}}{N_{total}} = \frac{S_{积分}}{S_{矩形}}$$

• 3.蒙特卡罗求解三门问题

三门问题(Monty Hall problem)大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率吗？如果严格按照上述的条件，即主持人清楚地知道，自己打开的那扇门后是羊，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。

在三门问题中，用 0、1、2分别代表三扇门的编号，在 $[0,2]$ 之间随机生成一个整数代表奖品所在门的编号 prize，再次在 $[0,2]$ 之间随机生成一个整数代表参赛者所选择的门的编号 guess。用变量 change 代表游戏中的换门($ture$)与不换门($false$)：

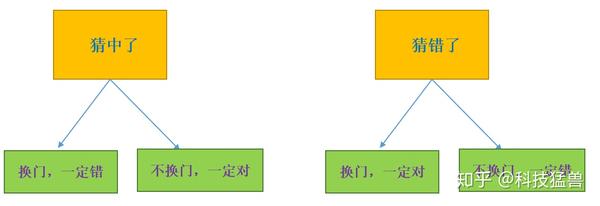
蒙特卡罗求解三门问题

这样大量重复模拟这个过程（10000次或者100000次）就可以得到换门猜中的概率和不换门猜中的概率。

使用python编程实现(程序太简单就省了，节约版面)，结果为：

玩1000000次,每一次都换门：
中奖率为：
0.667383
玩1000000次,每一次都不换门：
中奖率为：
0.333867

发现了吗？蒙特卡罗方法告诉我们，换门的中奖率竟是不换门的2倍。Why？

​ 蒙特卡罗求解三门问题理解

下面这个例子就能够让你理解这个问题：

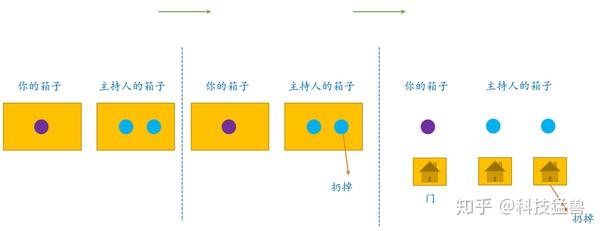
比如说主持人和你做游戏，你有一个箱子，里面有1个球；主持人一个箱子，里面有 $2$ 个球。他知道每个球的颜色，但你啥也不知道。但是 $3$ 个球里面只有 $1$ 个紫色的球，$2$ 个蓝色的球，谁手里面有紫色的球，谁就获得大奖。

主持人说：你要和我换箱子吗？

当然换，我箱子里只有1个球，中奖率 $\frac{1}{3}$ ，他箱子里有2个球，中奖率 $\frac{2}{3}$，换的中奖率是不换的 2 倍。

这是这个游戏的结论。现在情况变了：

主持人从他的箱子里扔了一个蓝色的球之后说：你要和我换箱子吗？

当然换，我箱子里只有1个球，中奖率 $\frac{1}{3}$，他箱子里有2个球，中奖率 $\frac{2}{3}$。扔了一个蓝色的，中奖率没变还是 ， $\frac{2}{3}$换的中奖率是不换的 2 倍。

这是这个游戏的结论。现在情况又变了：

没有箱子了，3个球之前摆了3扇门，只有一扇门后面是紫色的球，你只有1扇门，主持人有2扇，现在，主持人排除了一扇后面是蓝色球的门，再问你：你要和我换门吗？

这种情况和上一种一模一样，只不过去掉了箱子的概念，换成了门而已，当然这不是重要的，你也可以换成铁门，木门，等等。

所以还是换，我只有1个门，中奖率 $\frac{1}{3}$ ，他有2个门，中奖率 $\frac{2}{3}$。扔了一个没用的门，中奖率没变还是 ， $\frac{2}{3}$换的中奖率是不换的 2 倍。

Over！有点跑偏了，怎么说到三门问题上去了？？？本文想表达的只是蒙特卡罗方法可以帮助我们求解三门问题。

• 4.蒙特卡罗估计净利润

这个问题来自小学课本。

证券市场有时交易活跃，有时交易冷清。下面是你对市场的预测。

• 如果交易Slow，你会以平均价11元，卖出5万股。
• 如果交易Hot，你会以平均价8元，卖出10万股。
• 如果交易Ok，你会以平均价10元，卖出7.5万股。
• 固定成本12万。

已知你的成本在每股5.5元到7.5元之间，平均是6.5元。请问接下来的交易，你的净利润会是多少？

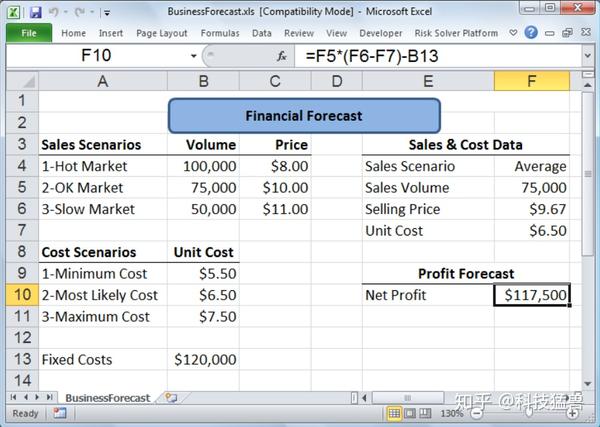
取1000个随机样本，每个样本有两个数值：一个是证券的成本(5.5元到7.5元之间的均匀分布)，另一个是当前市场状态(Slow、Hot、Ok，各有 $\frac{1}{3}$ 可能)。

蒙特卡罗估计净利润

模拟计算得到，平均净利润为92, 427美元。

计算方法是：1000次抽样，每次按均匀分布随机选定一个成本值、同时按1/3的概率选中一个市场情境，然后拿这两个参数可计算出净利润、平均利润，千次加总并取均值就是结果。

$$(4.5 \times 5 + 1.5 \times 10 + 3.5 \times 7.5) / 3 - 12 = 9.25(万)$$

问：这些例子的共同点是什么？

答：难度都不超过中学课本(~~~)。最重要的是，它们都是通过大量随机样本，去了解一个系统，进而得到所要计算的值。

正是由于它的这种特性，所以被称为统计模拟方法(statistical simulation method)，是通过从概率模型的随机抽样进行近似数值计算的方法。

其实随机算法分为两类：蒙特卡罗方法和拉斯维加斯方法，蒙特卡罗方法指的是算法的时间复杂度固定，然而结果有一定几率失败，采样越多结果越好。拉斯维加斯方法指的是算法一定成功，然而运行时间是概率的。

问：你有没有总结出蒙特卡罗方法的使用场景？

答：有。当所求解的问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种"实验"(或者说"计算机实验"的方法)，以事件出现的频率作为随机事件的概率(落在圆内的概率等)，或者得到这个随机变量的某些数字特征(积分值，净利润等)，并将其作为问题的解。

你也许忽然间明白了，蒙特卡罗方法应该这么用：

比如说我要求某个参量，直接求解遇到了困难，那我就构造一个合适的概率模型，对这个模型进行大量的采样和统计实验，使它的某些统计参量正好是待求问题的解，那么，只需要把这个参量的值统计出来，那么问题的解就得到了估计值。

随机抽样

通过上面的几个例子我们发现：蒙特卡罗法要解决的问题是：假设概率分布的定义已知，通过

抽样获得概率分布的随机样本，并通过得到的随机样本对概率分布的特征进行分析。比如，从

样本得到经验分布，从而估计总体分布；或者从样本计算出样本均值，从而估计总体期望。所

以蒙特卡罗法的核心是随机抽样(random sampling)。

可是，随机抽样(random sampling)的方法从来都不是一成不变的，在下面的这个例子里面，我会阐明马尔科夫方法的一般形式：

求解积分： $S = \int_{a}^{b}f(x)dx$

如果很难求出 $f(x)$ 的具体表达式，那么我们就需要用到蒙特卡洛方法。你可以如前文所述在二维空间中洒1000个点，看有多少落在积分区域的内部。也可以换种方式理解这个做法：

$$S = \int_a^bf(x)dx = \int_a^bp(x)\frac{f(x)}{p(x)}dx = E_{x \to p(x)[\frac{f(x)}{p(x)}]}$$

注意我们对这个积分表达式进行了一些trick，使它变成了一个对 $\frac{f(x)}{p(x)}$ 的期望，这个期望服从的分布是 $p(x)$。注意这个分布 可以 $p(x)$ 是任何一种概率分布。

下面如果想估计这个期望值，就需要按照概率分布 $p(x)$ 独立地抽取n个样本 $x_1, x_2, ..., x_n$。

注意，这里不是胡乱抽取 $n$ 个样本，而是按照概率分布 独$p(x)$立地抽取 $n$ 个样本。 $p(x)$ 不同，抽取样本的方式当然也不会相同。

辛勤大数定律告诉我们，当 $n \to +\infty$ 时，$\frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)} \to E_{x \to p(x)}[\frac{f(x)}{p(x)}]$

这句话的意思是说：我按照概率分布 $p(x)$ 独立地抽取 $n$ 个样本，只要把 $\frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)}$ 算出来，$E_{x \to p(x)}[\frac{f(x)}{p(x)}]$ 也就得到了。

一个特殊的情况是当按均匀分布抽取 $n$ 个样本时，即 $p(x) = \frac{1}{b-a}$

$$\frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)} = \frac{b-a}{n} \sum_{i=1}^{n}f(x_i)$$

这就是大一高数里面讲的积分的估计方法：

把积分区域等分为 n 份(均匀抽样)，每一份取一个点 $x_i$ ，计算出 $f(x_i)$ 取均值作为这一段积分的函数的均值，最后乘以积分区间的长度即 $b-a$可。

也就是蒙特卡罗方法的一个特例而已。

说了这么半天，它的基本思想就能用一个公式表达：

$\frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)} \to E_{x \to p(x)}[\frac{f(x)}{p(x)}]$，注意 $n$ 个点要按照 $p(x)$ 采样，且越大 $n$，越精确。

现在的问题转到了如何按照 $p(x)$ 采样若干个样本上来。但是，按照 $p(x)$ 采样绝非易事，因为有些时候我们根本不知道 是$p(x)$什么，或者有时候是一个很复杂的表达式，计算机没法直接抽样。

• 随机抽样方法1：拒绝-接受采样

这种方法适用于 $p(x)$ 极度复杂不规则的情况。

因为 $p(x)$ 没法直接采样，那我找一个可以直接采样的分布 $q(x)$ 作为媒介，这个媒介专业术语叫做建议分布(proposal distribution)，这个比如 $q(x)$ 说是一个高斯分布，且它的 $c$ 倍一定大于等于 $p(x)$ ，其中 $c > 0$ ，如下图所示：

​ 拒绝-接受采样

具体的做法是：首先按照 $q(x)$ 进行采样，比如说采样得到 $x^*$，还有一定的概率舍弃它。那么：

有多大的概率保留下来呢？$\frac{p(x^*)}{cq(x^*)}$

有多大的概率舍弃掉它呢？$1 - \frac{p(x^*)}{cq(x^*)}$

这样做的结果是：保留下来的每一个 $x^*$ 都相当于是按照 $p(x)$ 采样得到的 $x^*$ 了，直至得到 $n$ 个随机样本，结束。

• 问：为什么这样可以？
• 答：其实很好理解，如果 $p(x) = q(x)$ ，那么按照 $q(x)$ 进行采样之后的保留率为 $1$，没就相当于根据 $p(x)$ 采样 。如果 $p(x) \neq q(x)$ ，那么按道理如果按照 $p(x)$ 采样，这个点 $x^*$ 不一定被采 样到，所以我们设置了一个保留概率 $\frac{p(x^*)}{cq(x^*)}$ ，大于它才会保 留下来。且 $p(x^*)$ 越大，越容易被保 留下来。

• 随机抽样方法2：重采样技术 reparameterization trick

这个方法在 VAE 中经常使用，可以参考我之前的 Blog，这种方法适用于 $p(x)$ 是常见的连续分布，比如正态分布，$t$ 分布，$F$ 分布，$Beta$分布，$Gamma$分布等。

在 $VAE$ 中使用重采样技术是为了能让网络能够完成反向传播，具体是这样子：

现在要从 $N(\mu, \sigma^2)$ 中采样一个 $Z$ ， 相当于从 $N(0, 1)$ 中采样一个 $\epsilon$ ，然后让

$$Z = \mu + \epsilon \times \sigma$$

于是，我们将从 $N(\mu, \sigma^2)$ 采样变成了从 $N(0, 1)$ 中采样，然后通过参数变换得到从 $N(\mu, \sigma^2)$ 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

重参数技巧还可以这样来理解：
比如我有 $\frac{\part L}{\part Z}$ ，可是 $Z$ 是采样得到的，后向传播无法继续往前面求导了。
现在使用了重参数技巧以后，$Z = \mu + \epsilon \times \sigma$ 。 $\frac{\part L}{\part \sigma^2} = \frac{\part L}{\part Z}\frac{\part Z}{\part \sigma^2} = \frac{\part L}{\part Z} \epsilon$
这样就可以正常使用反向传播了。

所以说重采样技术的思想就是把复杂分布的采样转化为简单分布的采样，再通过一些变换把采样结果变回去。

再比如我要从二维正态分布中采样得到相互独立的 $X, Y \to N(\mu_1, \mu_2, \sigma^2_1, \sigma_2^2) = N(0, 0, 1, 1)$ ，我就可以先从均匀分布中采样两个随机变量 $U_1, U_2 \to U(0, 1)$ ，再通过下面的变换得到 $X, Y$ ：

$$X = \cos(2\pi U_1) \sqrt{-2lnU_2}$$

$$Y = \sin(2\pi U_1)\sqrt{-2ln U_2}$$

这个变换的专业术语叫做 Box-Muller 变换，它的证明如下：

证：假设相互独立的 $X, Y \to N(0,0,1,1)$ ，则：$X$ 的概率密度: $p(X) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ ， $Y$ 的概率密度：$p(Y) = \frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}}$
因为相 互独立，所以联合概率密度为: $p(X, Y) = \frac{1}{2\pi}e^{-\frac{x^2 + y^2}{2}}$
使用二重积分的经典套路，将 $X$、$Y$ 作坐标变换，使：

$$X = R\cos \theta$$

$$Y = R\sin \theta$$
得到：$p(R, \theta) = \frac{1}{2\pi}e^{-\frac{r^2}{2}}$

而且：$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \frac{1}{2\pi}e^{-\frac{x^2 + y^2}{2}}dXdY = \int_{0}^{2\pi}\int_{0}^{+\infty} \frac{1}{2\pi}e^{-\frac{r^2}{2}}rdrd\theta = 1$

算到这里要明确我们的目标是什么？

答：应该是反推出来随机变量 $U_1, U_2 \to U(0, 1)$ 。先看看 $R$ 和 $\theta$ 的概率分布和概率密度吧，根据概率论知识有：

$$F_R(r) = \int_{0}^{2\pi} \int_{0}^{r} \frac{1}{2\pi}e^{-\frac{r^2}{2}}rdrd\theta = 1 - e^{-\frac{r^2}{2}}$$

$$F_{\theta}(\varphi) = \int_{0}^{\varphi} \int_{0}^{+\infty}\frac{1}{2\pi}e^{-\frac{r^2}{2}}rdrd\theta = \frac{\varphi}{2\pi}$$

一眼就看出来 $\theta \to U(0, 2\pi)$ 。所以 $\theta = 2\pi U_1 = 2\pi U_2$ 。

接下来设 $Z = 1 - e^{-\frac{R^2}{2}}$ ，不知道 $Z$ 服从什么分布哦。

$$P(Z < z) = P(1 - e^{-\frac{R^2}{2}} <z) = P(R < \sqrt{-2ln(1-z)}) = F_R(\sqrt{-2ln(1-z)}) = z$$
所以 $Z = 1 - e^{-\frac{R^2}{2}} \to U(0, 1)$ ，现在知道了 $Z$ 服从均匀分布。
所以此时有 $1 - e^{-\frac{R^2}{2}} \to U(0, 1)$ ，即 $e^{-\frac{R^2}{2}} \to U(0, 1)$ ，即有： $R = \sqrt{-2lnU_1} = \sqrt{-2lnU_2}$
所以：

$$X = R\cos\theta = \cos(2\pi U_1) \sqrt{-2lnU_2}$$

$$Y = R\sin\theta = \sin(2\pi U_1)\sqrt{-2ln U_2}$$
Box-Muller变换得证。

至此，我们讲完了蒙特卡洛方法，这个方法非常强大和灵活，也很容易实现。对于许多问题来说，它往往是最简单的计算方法，有时甚至是唯一可行的方法。

从上面可以看出，要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，必须解决如何方便得到各种复杂概率分布的对应的采样样本集的问题。而马尔科夫链就能帮助你找到这些复杂概率分布的对应的采样样本集。

二. 马尔可夫链

在蒙特卡罗方法中，我们采集大量的样本，构造一个合适的概率模型，对这个模型进行大量的

采样和统计实验，使它的某些统计参量正好是待求问题的解。但是，我们需要大量采样，虽然

我们有拒绝-接受采样和重采样技术，但是依旧面临采样困难的问题。巧了，马尔科夫链可以

帮我们解决这个难题。

首先我们看一些基本的定义：

定义(马尔可夫链)：考虑一个随机变量的序列 $X = \{X_0, X_1, ..., X_t, ...\}$
这里 $X_t$表 示时刻 $t$的随 机变量，$t = 0, 1, 2, ...$ 。每 个随机变量 $X_t$的
取值 集合相同，称为状态空间，表示为 $S$ 。随机变 量可以是离散的，也可以是连续的。
以上随机变量的序列构成随机过程(stochastic process)。

假设在时刻的随机变量 $X_0$ 遵循概率分布 $P(X_0) = \pi_0$ ，称为初始状态分布。在某个时刻 $t \geq 1$ 的 随机变量 $X_t$ 与前一个时刻的随机变量 $X_{t-1}$ 之间有 条件分布 $P(X_t | X_{t-1})$ ，如果 $X_t$ 只依赖于 $X_{t-1}$ ，而不依赖于过去的随机变量 $\{X_0, X_1, ..., X_{t-2}\}$ ，这一性质称为 马尔可夫性，即：

$$P(X_t|X_{t-1}, X_{t-2}, ..., X_0) = P(X_t| X_{t-1}), t = 1, 2, ...$$
具有马尔可夫性的随机序列$X = {X_0, X_1, ..., X_t, ...}$ 称为马尔可夫链(Markov
chain)，或马尔可夫过程(Markov process)。条件概率分布 $P(X_t | X_{t-1})$ 称 为马尔可夫链的转移概率分布。转移概率分布决定了马尔可夫链的特性。

如果这个条件概率分布与具体的时刻 $t$ 是无关的，则称这个马尔科夫链为时间齐次的马尔可夫链(time homogenous Markov chain)。

定义：转移概率矩阵：

$$P = \left[ \begin{matrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23}\\ p_{31} & p_{32} & p_{33}\end{matrix} \right]$$

其中 $p_{ij} = P(X_t = i | X_{t-1} = j)$ 。

定义：马尔科夫链在 $t$ 时刻的概率分布称为 $t$ 时刻的状态分布：

$$\pi(t) = \left[ \begin{matrix} \pi_1(t)\\ \pi_2(t) \\ \pi_3(t)\end{matrix} \right]$$

其中 $\pi_i(t) = P(X_t = i), i = 1, 2, ....$ 。

特别地，马尔可夫链的初始状态分布可以表示为：

$$\pi(0) = \left[ \begin{matrix} \pi_1(0)\\ \pi_2(0) \\ \pi_3(0)\end{matrix} \right]$$

通常初始分布 $\pi(0)$ 向量只有一个分量是 $1$，其余分量都是 $0$，表示马尔可夫链从一个具体状态开始。

有限离散状态的马尔可夫链可以由有向图表示。结点表示状态，边表示状态之间的转移，边上的数值表示转移概率。从一个初始状态出发，根据有向边上定义的概率在状态之间随机跳转(或随机转移)，就可以产生状态的序列。马尔可夫链实际上是刻画随时间在状态之间转移的模型，假设未来的转移状态只依赖于现在的状态，而与过去的状态无关。

下面通过一个简单的例子给出马尔可夫链的直观解释：如下图王者荣耀玩家选择英雄的职业的转变，转移概率矩阵为：

$$P = \left[ \begin{matrix} 2.5 & 0.5 & 0.25 \\ 0.25 & 0 & 0.25\\ 0.25 & 0.5 & 0.5\end{matrix} \right]$$

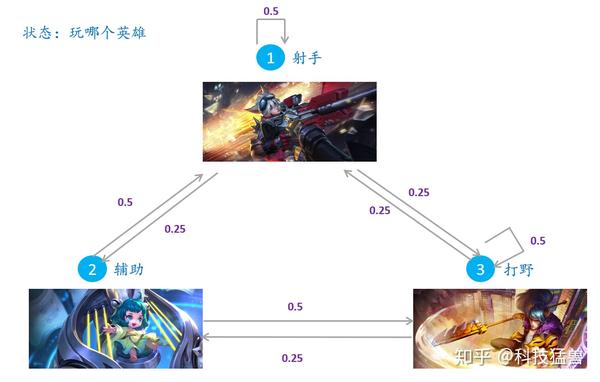王者荣耀玩家选择英雄的职业的转变

我们试图用程序去模拟这个状态的变化情况，任意假设一个初始状态：设初始的三个概率分别是 $[0.5, 0.3, 0.2]$ ，即 $t_0$时 刻，50% 概率选择射手，30% 概率选择辅助，20% 概率选择打野，将此代入转移概率，我们一直计算到 $t_{100}$ 看看 是什么情况：

import numpy as np
import matplotlib.pyplot as plt
transfer_matrix = np.array([[0.5,0.5,0.25],[0.25,0,0.25],[0.25,0.5,0.5]],dtype='float32')
start_matrix = np.array([[0.5],[0.3],[0.2]],dtype='float32')

value1 = []
value2 = []
value3 = []
for i in range(30):
    start_matrix = np.dot(transfer_matrix, start_matrix)
    value1.append(start_matrix[0][0])
    value2.append(start_matrix[1][0])
    value3.append(start_matrix[2][0])
print(start_matrix)

x = np.arange(30)
plt.plot(x,value1,label='Archer')
plt.plot(x,value2,label='Support')
plt.plot(x,value3,label='Assassin')
plt.legend()
plt.show()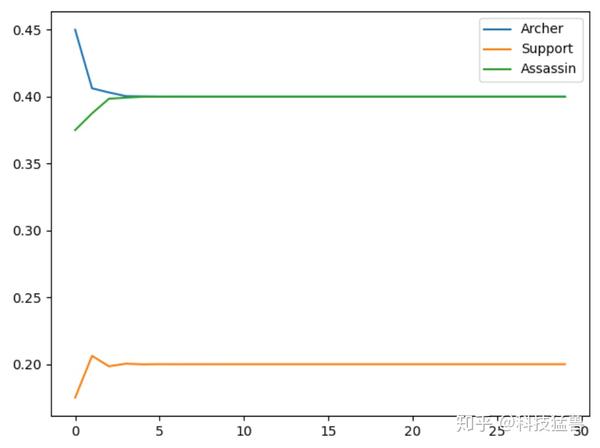

可以发现，从5轮左右开始，我们的状态概率分布就不变了，一直保持在：

[[0.4       ]
 [0.19999999]
 [0.39999998]]

从这个实验我们得出了一个结论：这个玩家如果一直把王者荣耀玩下去，他最后选择射手，辅助，打野的概率会趋近于：$[0.4, 0.2, 0.4]$ ，很有意思的结论。

• 问：是不是所有马尔科夫链都有平稳分布？

答：不一定，必须满足下面的定理：

定理：给定一个马尔科夫链 $X = \{X_0, X_1, ..., X_t, ...\}$ ，$t$ 时刻的状态分布：$\pi = (\pi_1, \pi_2, ...)$ 是 $X$ 的平稳分布的条件是 是下列$\pi = (\pi_1, \pi_2, ...)$方程组的解：

$$x_i = \sum_j p_{ij}x_j, i = 1, 2, ...$$

$$x_i \geq 0, i = 1, 2, ...$$

$$\sum_i x_i = 1$$
证：
必要性：假设 $\pi = (\pi_1, \pi_2, ...)$ 是平稳分布，则显然满足后2式，根据平稳分布的性质，$\pi_i = \sum_j p_{ij}\pi_j, i = 1, 2..$ ，满足1式，得证。
充分性：假设 $\pi = (\pi_1, \pi_2, ...)$为$X_t$ 的分布， 则：

$$P(X_t = i) = \pi_i = \sum_j p_{ij} \pi_j = \sum_j p_{ij}P(X_{t-1} = j), i = 1, 2$$
所以 $\pi = (\pi_1, \pi_2, ...)$也为 $X_{t-1}$的分 布，又因为对任意的 $t$成立， 所以 $\pi = (\pi_1, \pi_2, ...)$是平稳分布。

马尔科夫链的性质

• 不可约

一个不可约的马尔可夫链，从任意状态出发，当经过充分长时间后，可以到达任意状态。数学语言是：

定义：给定一个马尔科夫链 $X = \{X_0, X_1, ..., X_t, ...\}$ ，对于任意的状态 $i \in S$ ，如果存在一个时刻 $t$满足 ：$P(X_t = i | X_0 = j) > 0$ ，也就是说，时刻 $0$ 从状态 $j$ 出发，时刻 $t$ 到达状态 $i$ 的概率大于０，则称此马尔可夫链 $X$是不可约的 (irreducible)，否则称马尔可夫链是可约的(reducible)。

可约的马尔科夫链

• 非周期

定义：给定一个马尔科夫链 $X = \{X_0, X_1, ..., X_t, ...\}$ ，对于任意的状态 $i \in S$ ，如果时刻 $0$从状 态 $i$ 出发，$t$ 时刻返 回状态的所有时间长 $\{t : P(X_t = i | X_0 = i) > 0\}$ 的最大公约数是 $1$，则称此马尔可夫链 $X$ 是非周期的， 否则称马尔可夫链是周期的。

周期的马尔科夫链

• 定理：不可约且非周期的有限状态马尔可夫链，有唯一平稳分布存在。

定义：首达时间：

$T_{ij} = min\{n : n \geq 1, X_0 = i, X_n = j\}$ 表示从状态 $i$ 出发首次到达状态 $j$ 的时间。若状态 $i$ 出发 永远不能到达状态 $j$ ，则 $T_{ij} = + \infty$ 。

定义：首达概率：

**

$f_{ij}^{(n)} = P(X_n = j, X_m \neq j, m = 1, 2, ..., n-1|X_0 = i)$

$f_{ij}^{(n)}$ 为从状态 $i$ 出发经过 $n$步首 次到达状态 $j$ 的概率 。

$f_{ij}^{+\infty}$ 为从状态 $i$ 出发永远不能到达状态 $j$ 的 概率。

定义：从状态 $i$ 出发经过有限步首次到达状态 $j$ 的概率：

$$f_{ij} = \sum_{n=1}^{+\infty}f_{ij}^{(n)} = P(T_{ij} < + \infty)$$

定义：

状态 $i$ 为常返态： $f_{ii} = 1$ ，即有限步一定能回来。

状态 $i$ 为常返态： $f_{ii} < 1$ ，即有限步可能回不来。

定义：平均返回时间：

$$\mu_i = \sum_{n=1}^{+\infty}nf_{ii}^{n}$$

• 正常返和零常返

首先 $i$ 得是常返态，且若 $\mu_i < + \infty$ ，称状态 $i$ 为正常返。若 $\mu_i = + \infty$ ，称状态 $i$ 为零常返。

• 遍历态

![[公式]](https://www.zhihu.com/equation?tex=i) 既是正常返又是非周期，就是遍历态。

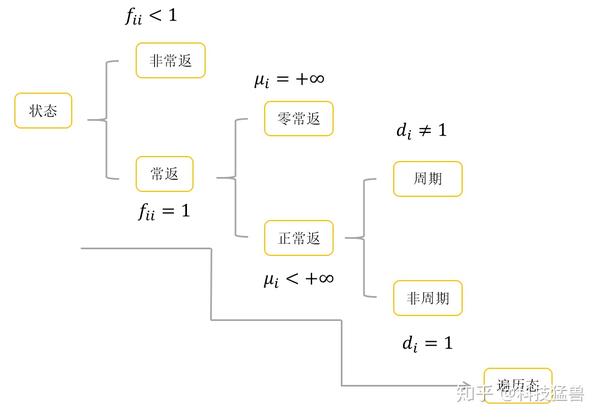各种定义汇总

直观上，一个正常返的马尔可夫链，其中任意一个状态，从其他任意一个状态出发，当时间趋于无穷时，首次转移到这个状态的概率不为0。(从任意一个状态出发，走了能回来)

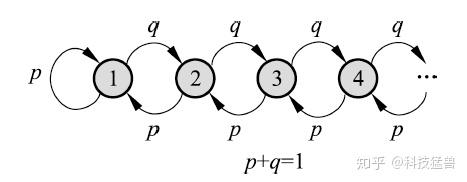清华大学随机过程期末考试题：这个马尔科夫链是正常返的吗？

如上图所示的马尔科夫链，当 $p > q$ 时是正常返的，当 $p < q$ 时不是正常返的。

证：转移概率矩阵：
![[公式]](https://www.zhihu.com/equation?tex=P%3D%5Cbegin%7Bbmatrix%7Dp+%26+p+%260%260%26...+%5C%5C+q+%26+0+%26p%260%26...+%5C%5C++0+%26+q+%260%26p%26...%5C%5C++0+%26+0+%26q%260%26...%5C%5C++...+%26+...+%26...%26...%26...%5Cend%7Bbmatrix%7D)
若达到了平稳分布，则 $P\pi = \pi$ ，代入 $P$ 化简，且注意 $p + q = 1$ 。

$$\pi_2 = \frac{q}{p}\pi_1, \pi_3 = \frac{q}{p}\pi_2, \pi_4 = \frac{q}{p}\pi_3, ...$$

$$\pi_1 + \pi_2 + \pi_3 + ... = 1$$
当 $p > q$ 时，平稳分布是：$\pi_i = (\frac{q}{p})^i(\frac{p-q}{p}), i = 1, 2, ...$
当时间趋于无穷时，转移到任何一个状态的概率不为 0，马尔可夫链是正常返的。
当 $p < q$ 时，不存在平稳分布，马尔可夫链不是正常返的。
你看，清华的期末考试也不过如此~

• 遍历定理：不可约、非周期且正常返的马尔可夫链，有唯一平稳分布存在，并且转移概率的极限分布是马尔可夫链的平稳分布。

$$lim_{t \to + \infty}P(X_t = i|X_0=j)=\pi_i, i = 1, 2, ...; j = 1, 2, ...$$

你会发现，不可约、非周期且正常返的马尔可夫链，它的转移概率矩阵在 $t \to + \infty$ 时竟然是：

![[公式]](https://www.zhihu.com/equation?tex=%5Cunderset%7Bn%5Crightarrow+%5Cinfty%7D%7Blim%7DP%5E%7Bn%7D%3D%5Cbegin%7Bbmatrix%7D%5Cpi%281%29+%26%5Cpi%281%29+%26%5Ccdots+%26%5Cpi%281%29+%26+%5Ccdots+%5C%5C+%5Cpi%282%29+%26%5Cpi%282%29+%26%5Ccdots+%26%5Cpi%282%29+%26+%5Ccdots+%5C%5C+%5Cvdots+%26+%5Cvdots+%26+%5Cvdots+%26%5Cddots+%26%5Cvdots+%5C%5C+%5Cpi%28j%29+%26%5Cpi%28j%29+%26%5Ccdots+%26%5Cpi%28j%29+%26+%5Ccdots+%5C%5C+%5Cvdots+%26+%5Cvdots+%26+%5Cvdots+%26+%5Cddots+%26+%5Cvdots+%5Cend%7Bbmatrix%7D)

今后，你如果再遇到某个题目说“一个满足遍历定理的马尔科夫链，...”你就应该立刻意识到这个马尔科夫链只有一个平稳分布，而且它就是转移概率的极限分布。且随机游走的起始点并不影响得到的结果，即从不同的起始点出发，都会收敛到同一平稳分布。注意这里很重要，一会要考。

说了这么多概念，用大白话做个总结吧：

• 不可约：每个状态都能去到。
• 非周期：返回时间公约数是1。
• 正常返：离开此状态有限步一定能回来。迟早会回来。
• 零常返：离开此状态能回来，但需要无穷多步。
• 非常返：离开此状态有限步不一定回得来。
• 遍历定理：不可约，非周期，正常返 ![[公式]](https://www.zhihu.com/equation?tex=%5Crightarrow) 有唯一的平稳分布。

• 可逆马尔可夫链

定义：给定一个马尔科夫链 $X = {X_0, X_1, ..., X_t, ...}$ ，如果有状态分布 $(\pi_1, \pi_2, \pi_3, ...)$ 。对于任意的状态 $i, j \in S$ ，对任意一个时刻 $t$ 满足 ：

$$P(X_t = i|X_{t-1}=j)\pi_j = P(X_t=j|X_{t-1}=i)\pi_i, i = 1, 2, ...$$
或简写为：

$$p_{ij}\pi_j = p_{ji}\pi_i$$

则称此马尔可夫链 $X$ 为可逆马尔可夫链(reversible Markov chain)，上式称为
细致平衡方程(detailed balance equation)。
直观上，如果有可逆的马尔可夫链，那么以该马尔可夫链的平稳分布作为初始分布，进行随机状态转移，无论是面向未来还是面向过去，任何一个时刻的状态分布都是该平稳分布。概率分布 $\pi$ 是状态转移矩阵 $P$ 的平稳分布。
定理：满足细致平衡方程的状态分布 $\pi$ 就是该马尔可夫链的平稳分布 $P\pi = \pi$ 。
证：
$$(P\pi)_i = \sum_j p_{ij}\pi_j = \sum_j p_{ij}\pi_{i} = \pi_i \sum_{j}p_{ij} = \pi_i, i = 1, 2, ...$$

以上就是关于蒙特卡罗方法和马尔科夫链你分别需要掌握的知识，说了这么久还没有进入正题。本文是为了让你打好基础，那从下一篇文章开始，我们会讲解什么是马尔科夫链蒙特卡罗方法以及它的具体细节。

参考：

《统计学习方法》(李航)

蒙特·卡罗方法_百度百科

蒙特卡罗方法入门 - 阮一峰的网络日志

MCMC(一)蒙特卡罗方法 - 刘建平Pinard

作者：科技猛兽
链接：https://zhuanlan.zhihu.com/p/250146007
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。